Inversions in an array

Inversions : Number of pairs (i,j) such that i < j and arr[i] > arr[j] .

Now lets see how to find number of such pairs.

The Brute Way O(N^2)

We will traverse array for each pair i,j and check if arr[i]>arr[j] .

int count = 0;

for(int i=0;i<N;i++)

for(int j=i+1;j<N;j++)

if(arr[j]<arr[i])  count++;

The count will store our answer.

A Smart Way O(N logN)

We can use modified merge sort to find number of inversions in an array.

As we know in merge sort we keep on dividing the array then we sort those parts and then merge those sorted parts, we can modify the algorithm by adding just a variable that will keep on adding count of inversions.

Now we know when we are merging two parts number of inversions are sum of inversions in both those parts and the number of inversions in the merge operation.

Now the main trick and heart of algorithm lies in the merge part and lets see how to calculate that :

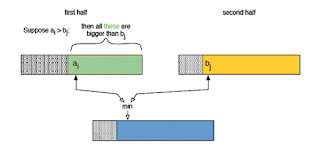
As we can see both these parts are sorted, so for a specific j if arr[j] < arr[i] all elements between mid and i will be greater than j, since both arrays are sorted, so we need to add (mid-i) to the count of inversions.

Here is a sample code for better understanding :

public  int merge_sort(int left, int right) {

int count = 0;

if (right > left) {

int mid = (right + left) / 2;

count = merge_sort(left, mid);

count += merge_sort(mid + 1, right);

count += merge(left, mid + 1, right);

}

return count;

}

public  int merge(int left, int mid, int right) {

int count=0;

int i=left,j=mid,k=left;

while((i<mid)&&(j<=right))

{

if(arr[i]<=arr[j]) temp[k++]=arr[i++];

else {

temp[k++]=arr[j++];

count+=(mid-i);

}

}

while(i<mid) temp[k++]=arr[i++];

while(j<=right) temp[k++]=arr[j++];

for(i=left;i<=right;i++) arr[i]=temp[i];

return count;

}

Another Smart Way : BIT O(N log N)

This problem can also be solved using a BIT (Binary Indexed Tree). Lets see how to do that.

Basically using a BIT we can find cumulative sum till an index i in logn time.We will use this property to count the number of inversions.

Here is a simple implementation of BIT :

  class BIT

{

int tree[];

public BIT(int n)

{

tree=new int[n+1];      //only for this case else construct properly.

}

public int sum(int i)

{

int sum=0;

while(i>0)

{

sum+=tree[i];

i -= (i & -i);

}

return sum;

}

public void update(int i,int x)

{

while(i<tree.length)

{

tree[i]+=x;

i += (i & -i);

}

}

 }

Now basically we will see count of all i such that arr[i]<arr[j] which we can get from BIT easilly, we need the opposite so we can keep on adding i-sum(i) to our count which will give us the number of inversions.

Here is the sample code to do that :

  BIT bit=new BIT(arr.length);

int tempo[]=arr.clone();

Arrays.sort(tempo);

int res=0;

for(int i=0;i<arr.length;i++)

{

int ind=Arrays.binarySearch(tempo, arr[i])+1;

res+=(i-bit.sum(ind));

bit.update(ind, 1);

}

Hope you enjoy it !!!